Training School on
Physics and Mathematics of Topological Textures
12-13 May 2025 | Budapest, Hungary

Deadlines
14 March 2025:
Application28 March 2025:
Notification regarding participation acceptance.
Invitations to be sent via the e-COST platform.2 April 2025:
Finalization of the participant list.9 April 2025:
Final program published on the website.
Aim
- Introduction to the physics and mathematics of topological textures in magnetics, condensed matter and light.
- Train early stage researchers on research topics related to topological textures from a broad perspective in condensed matter and light.


Courses
Markus Garst, Karlsruhe Institute of Technology, Germany.
The aim of these lectures will be an introduction to topological textures from the perspective of magnetism. We start with a summary of the quantum mechanics of spin operators and the Heisenberg Hamiltonian describing the interaction between distinct quantum spins on a discrete lattice. Afterwards, the notion of the spin-path integral and its corresponding action will be introduced. The dynamical part of the action is given by a Berry phase and it will be discussed how it recovers the Landau-Lifshitz equation on the classical level. We will discuss the continuum approximation of the action and its relation to the field of micromagnetics. We continue with an introduction of topological configurations of the magnetization field and its classification in terms of homotopy groups. We discuss topological defects like vortices and hedgehogs, i.e., Bloch points, for which the magnetization vanishes at the center of the defect. Finally, we introduce topological textures, for which the magnetization is well defined at every point in space. This includes domain walls, merons, skyrmions and hopfions. We give examples of materials where such textures have been already identified.
Radu Ignat, Université Paul Sabatier, Toulouse, France.
Vortices are topological textures that appear in many physical systems (superconductivity, superfluids, ferrromagnetics, liquid crystals etc.)
We will present the analysis of vortices in a two dimensional Ginzburg-Landau (GL) model that is the prototype in several variational problems.
This toy model depends on a small parameter epsilon and it is related to the harmonic map problem for unit length vector fields as epsilon tends to 0.
We will study ground states of (GL) for a given boundary data that carries a topological charge and induces the nucleation of vortices.
Several mathematical tools will be introduced for this study such as the topological degree, the jacobian of the ground state (detecting the vortices) as well as the renormalized energy
between vortices (determining their optimal location).
References:
1. F. Bethuel, H. Brezis and F. Hélein, Asymptotics for the minimization of a Ginzburg-Landau functional, Calc. Var. PDE 1 (1993), 123–148.
2. F. Bethuel, H. Brezis and F. Hélein, Ginzburg-Landau vortices, Birkhäuser Boston Inc., 1994.
3. F. B. Hang and F. H. Lin, Static theory for planar ferromagnets and antiferromagnets, Acta Math. Sin. (Engl. Ser.), 17 (2001), 541–580.
4. R. Ignat, L. Nguyen, V. Slastikov and A. Zarnescu, On the uniqueness of minimisers of Ginzburg-Landau functionals, Ann. Sci. Éc. Norm. Supér. 53 (2020), 589-613.
Radu Ignat, Université Paul Sabatier, Toulouse, France.
Domain walls are topological solitons that appear in many physical systems (phase transitions, condensed matter etc). They represent transition layers between two states corresponding to the wells of a certain potential function. We will start by presenting the domain walls in the Allen-Cahn model where the potential has a finite number of wells; in particular, we will study their symmetry and energy level. Next we study the case of Ginzburg-Landau type models where the potential has a continuum of wells. For well-posedness, the divergence-free constraint is imposed on the order parameter. In this case, we will study one-dimensional symmetry of domain walls as well as the nucleation of microstructures according to the shape of the potential function. Finally, we will discuss several type of domain walls in ferromagnetics (such as Bloch wall, cross-tie wall and zigzag wall).
References:
1. F. Alouges, T. Rivière, and S. Serfaty. Néel and cross-tie wall energies for planar micromagnetic configurations. ESAIM Control Optim. Calc. Var. 8 (2002), 31–68.
2. A. DeSimone, R.V. Kohn, S. Müller and F. Otto, Recent analytical developments in micromagnetics. The science of hysteresis 2 (2006) (4), 269–381.
3. A. Hubert and R. Schafer. Magnetic domains : The Analysis of Magnetic Microstructures, volume 21. Springer-Verlag, 1998.
4. R. Ignat and B. Merlet. Lower bound for the energy of Bloch walls in micromagnetics.
Arch. Ration. Mech. Anal. 199 (2011) (2), 369–406.
5. R. Ignat and R. Moser. A zigzag pattern in micromagnetics. J. Math. Pures Appl. 98 (2012), 139–159.
6. R. Ignat and A. Monteil, A DeGiorgi type conjecture for minimal solutions to a nonlinear Stokes equation, Comm. Pure Appl. Math. 73 (2020), 771-854
7. O. Savin. Regularity of flat level sets in phase transitions. Annals of Mathematics 169 (2009), 41–78.
Sonja Franke-Arnold, University of Glasgow, U.K.
Light beams and even single photons can be controlled in all their degrees of freedom, allowing us to create complex topological structures. These 2D and 3D optical fields may exist in free space, unrestricted by material symmetries or energy considerations, allowing us to construct optical structures reminiscent of those in condensed matter, but also to explore new configurations. The first tutorial will introduce a variety of methods for shaping, manipulating and analysing light, including polarisation optics, diffractive and refractive elements, but also computer controllable devices including spatial light modulators and digital mirror displays. In the second tutorial, we will concentrate on optical skyrmions and related structures, highlight some of their definitions and properties, and discuss how they can be measured based on Stokes tomography.
Filipp Rybakov, University of Uppsala, Sweden.
In the first part, we will discuss gradient-based minimization methods. We will focus on the conjugate gradient method and ways to preserve the "spins on unit spheres" constraint. In the second part we will discuss spatial discretization methods, especially recipes for taking into account dipole-dipole interactions.
Program
Time | Monday, May 12, 2025 | Tuesday, May 13, 2025 |
|---|---|---|
|
09:00 |
Theory of magnetism |
Mathematical analysis of domain walls |
|
10:30 |
Coffee break |
Coffee break |
|
11:00 |
Magnetic materials |
Structured light: |
|
12:30 |
Lunch break |
Lunch break |
|
14:00 |
Mathematical analysis of vortices |
Optical skyrmions: |
|
15:00 |
Coffee break |
Coffee break |
|
15:10 |
Discussion session |
Discussion session |
|
15:50 |
Coffee break |
Coffee break |
|
16:00 |
Practicals session |
Practicals: |
|
17:00 |
|
Poster session |
|
20:00 |
Dinner |
|
Venue
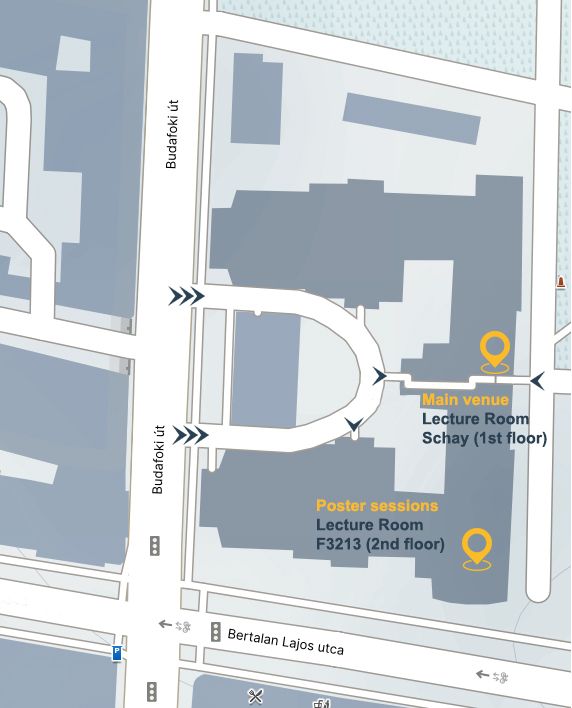
The training school will be held at the Budapest University of Technology and Economics
(Budafoki út 8., 1111 Budapest, Hungary).
Travel information
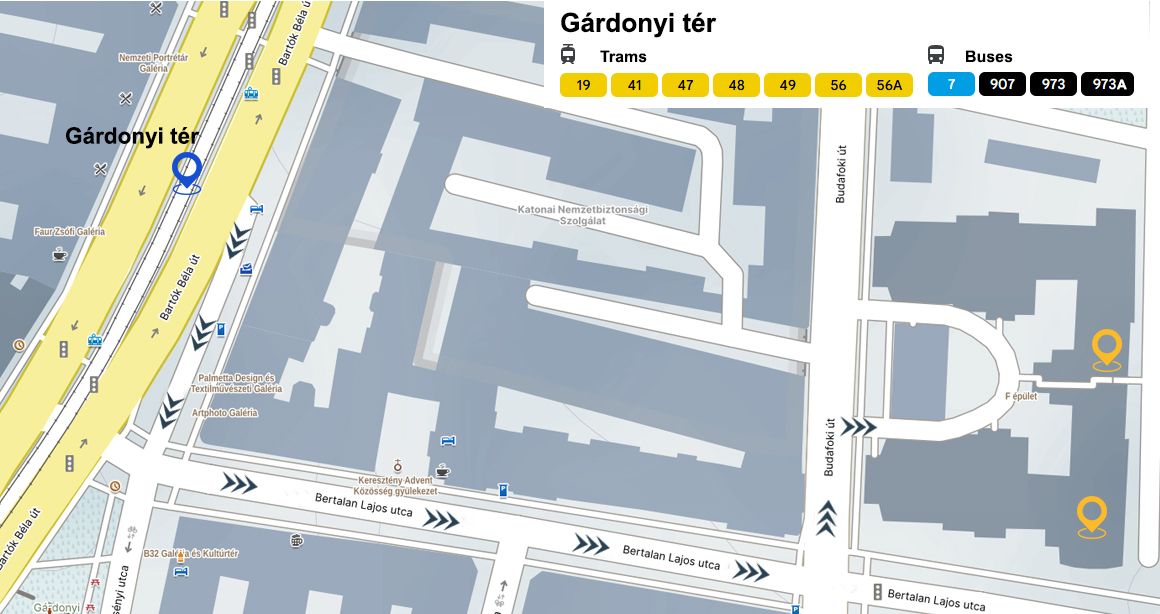
Budapest Airport may be reached by direct flights from many cities. It is located around 20 km from the city centre which may be reached by taxi, shuttle, express bus (100E) or by public transport (bus 200E connects to metro line M3).
Budapest may also be reached by train from Central European countries, and the main railway stations are located close to the city centre.
Budapest University of Technology and Economics is located on the bank of the river Danube. There are several hotels within walking distance on both sides of the river. It is also accessible by public transport, including metro line M4 and several tram lines.

Budapest University of Technology and Economics
Budafoki út 8., 1111 Budapest, Hungary
Important notes
-
Registration Fee
There is no registration fee. Participation includes access to the program book, session attendance, conference services, and coffee breaks.
-
Personal Arrangements
Participants are responsible for arranging their own accommodation, lunches, and dinners.
Beware of scam attempts! We do not collaborate with any 'housing' companies for accommodation services. -
Entry Requirements
-
Budget Allocation
The available budget will be allocated in accordance with the COST Excellence and Inclusiveness Policy.
-
Notification of Support
Decisions regarding COST support will be communicated to participants well in advance of the workshop to allow sufficient time for travel arrangements.
-
Travel Reimbursement and Daily Allowance
The maximum reimbursement for long-distance travel and the daily allowance rate, as specified in the COST Annotated Rules, may be adjusted following a decision by the Management Committee.
Did you receive an invitation through e-COST to participate in the training school on May 12-13 in Budapest? Does your invitation indicate that you are eligible for financial support? Read here the procedure to follow!
Organising Committee
- Bruno Barton-Singer, FORTH, Heraklion, Greece.
- Annika Johansson, Max Planck Institute of Microstructure Physics, Halle, Germany.
- Stavros Komineas, University of Crete & FORTH, Heraklion, Greece.
Local Organising Committee
- Krisztián Palotás, HUN-REN Wigner Research Center for Physics, Budapest, Hungary.
- Levente Rózsa, HUN-REN Wigner Research Center for Physics, Budapest, Hungary.
